Measurement and Scientific Tools
Description and Explanation
How would you describe the squirrel’s activity in Figure 1? A description is a spoken or written summary of observations. Your description might include information such as: the squirrel buried five acorns near a large tree. A qualitative description uses your senses (sight, sound, smell, touch, taste) to describe an observation. A large tree is a qualitative description. However, a quantitative description uses numbers to describe the observation. Five acorns is a quantitative description. You can use measuring tools, such as a ruler, a balance, or a thermometer, to make quantitative descriptions.
How would you explain the squirrel’s activity? An explanation is an interpretation of observations. You might explain that the squirrel is storing acorns for food at a later time. When you describe something, you report what you observe. But when you explain something, you try to interpret your observations. This can lead to a hypothesis.
Richard Peters/Alamy
Figure 1 A description and an explanation of a squirrel’s activity contain different information.
The International System of Units
Suppose you observed a squirrel searching for buried food and recorded that it traveled about 200 ft from its nest. Someone who measures distances in meters might not understand how far the squirrel traveled. The scientific community solved this problem in 1960. It adopted an internationally accepted system for measurement called the International System of Units (SI).
SI Base Units and Prefixes
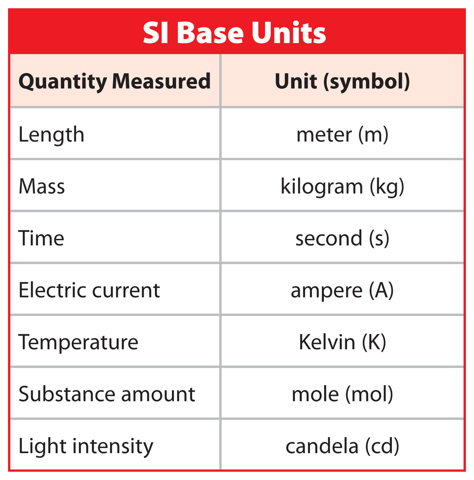
Like scientists and many others around the world, you probably use the SI system in your classroom. All SI units are derived from seven base units, as listed in Table 1. For example, the base unit for length, or the unit most commonly used to measure length, is the meter. However, you have probably made measurements in kilometers or millimeters before. Where do these units come from?
PETE OXFORD/MINDEN PICTURES/National Geographic Stock
Figure 2 Scientists use the SI system when taking measurements.
Table 1 SI Base Units
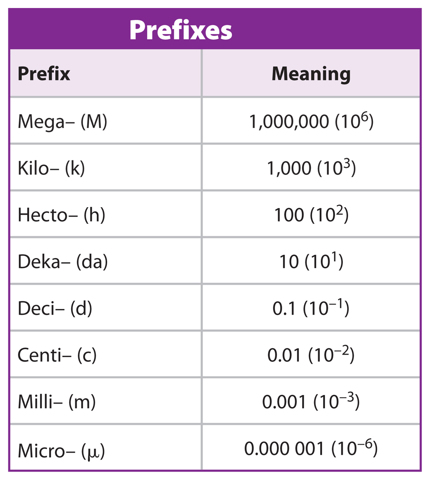
A prefix can be added to a base unit’s name to indicate either a fraction or a multiple of that base unit. The prefixes are based on powers of ten, such as 0.01 and 100, as shown in Table 2. For example, one centimeter (1 cm) is one one-hundredth of a meter and a kilometer (1 km) is 1,000 meters.
Table 2 Prefixes
Figure 3 SI units can be converted easily from one unit to another.
Precision and Accuracy
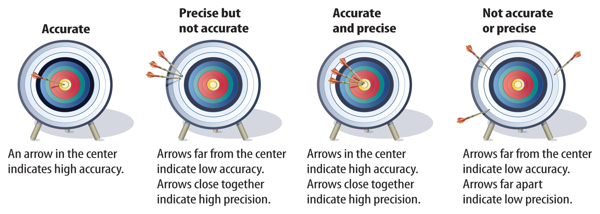
Suppose your friend Simon tells you that he will call you in one minute, but he calls you a minute and a half later. Sarah tells you that she will call you in one minute, and she calls exactly 60 seconds later. What is the difference? Sarah is accurate and Simon is not. Accuracy is a description of how close a measurement is to an accepted or true value. However, if Simon always calls about 30 seconds later than he says he will, then Simon is precise. Precision is a description of how similar or close measurements are to each other, as shown in Figure 4.
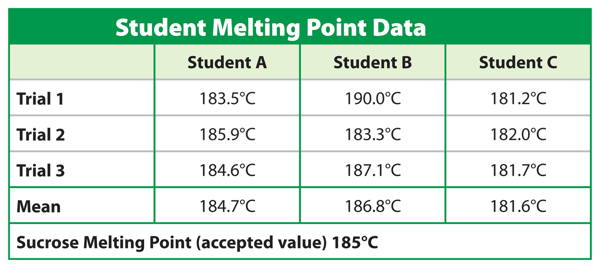
Table 3 illustrates the difference between precise and accurate measurements. Students were asked to find the melting point of sucrose, or table sugar. Each student took three temperature readings and calculated the mean, or average, of his or her data. As the recorded data in the table shows, student A had more accurate data. The melting point mean, 184.7°C, is closer to the scientifically accepted melting point, 185°C. Although not accurate, Student C’s measurements are the most precise because they are similar in value.
1. Key Concept Check How do accuracy and precision differ?
Figure 4 The archery target illustrates accuracy and precision. An accurate shot is in the bull’s-eye.
Table 3 The data taken by student A are more accurate because each value is close to the accepted value. The data taken by student C are more precise because the data are similar.
Measurement and Accuracy
The tools used to take measurements can limit the accuracy of the measurements. Suppose you are measuring the temperature at which sugar melts, and the thermometer’s measurements are divided into whole numbers. If your sugar sample melts between 183°C and 184°C, you can estimate the temperature between these two numbers. But, if the thermometer’s measurements are divided into tenths, and your sample melts between 183.2°C and 183.3°C, your estimate between these numbers would be more accurate.
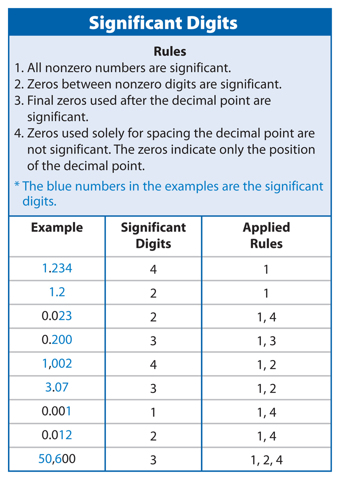
Significant Digits
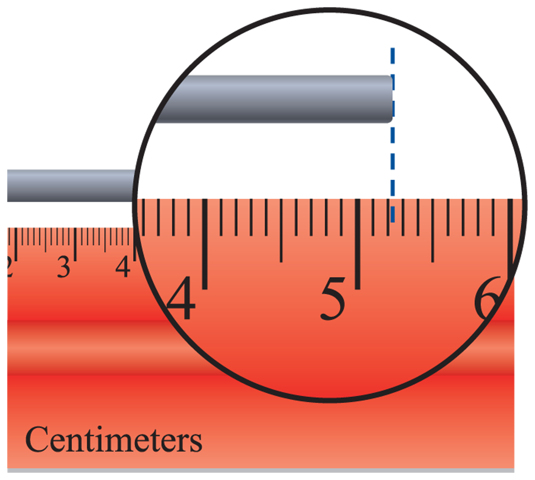
In the second example above, you know that the temperature is between 183.2°C and 183.3°C. You could estimate that the temperature is 183.25°C. When you take any measurement, some digits you know for certain and some digits you estimate. Significant digits are the number of digits in a measurement that are known with a certain degree of reliability. The significant digits in a measurement include all digits you know for certain plus one estimated digit. Therefore, your measurement of 183.25°C would contain five significant digits, as explained in Table 4. Using significant digits lets others know how certain your measurements are. Figure 5 shows an example of rounding to 3 significant figures.
1. Key Concept Check Why should you use significant digits?
Table 4 Significant Digits
Figure 5 Since the ruler is divided into tenths, you know the rod is between 5.2 cm and 5.3 cm. You can estimate that the rod is 5.25 cm.
Math Skills: Significant Digits
The number 5,281 has 4 significant digits. Rule 1 in Table 4 above states that all nonzero numbers are significant.
1. Practice
Use the rules in Table 4 to determine the number of significant digits in each of the following numbers: 2.02; 0.0057; 1,500; and 0.500.
Use the rules in Table 4 to determine the number of significant digits in each of the following numbers: 2.02; 0.0057; 1,500; and 0.500.
SCIENCE USE V. COMMON USE
digital
Science Use of, pertaining to, or using numbers (numerical digits)
Science Use of, pertaining to, or using numbers (numerical digits)
Common Use of or pertaining to a finger or toe
Scientific Tools
Scientific inquiry often requires the use of tools. Scientists, including life scientists, might use the tools listed below. You might use one or more of them during a scientific inquiry, too. For more information about the proper use and care of microscopes, see the Reference Handbook. For more information on other scientific tools, see the Science Skill Handbook.
Science Journal
In a science journal, you can record descriptions, explanations, plans, and steps used in a scientific inquiry. A science journal can be a spiral-bound notebook or a loose-leaf binder. It is important to keep your science journal organized so that you can find information when you need it. Make sure you keep thorough and accurate records.
Matt Meadows
Balances
You can use a triple-beam balance or an electric balance to measure mass. Mass usually is measured in kilograms (kg) or grams (g). When using a balance, do not let objects drop heavily onto the balance. Gently remove an object after you record its mass.
Charles D. Winters/Photo Researchers
Louis Rosenstock/The McGraw-Hill Companies
Thermometer
A thermometer measures the temperature of substances. Although the Kelvin (K) is the SI unit for temperature, in the science classroom, you measure temperature in degrees Celsius (°C). Use care when you place a thermometer into a hot substance so that you do not burn yourself. Handle glass thermometers gently so that they do not break. If a thermometer does break, tell your teacher immediately. Do not touch the broken glass or the thermometer’s liquid. Never use a thermometer to stir anything.
Biosphoto/NouN/Peter Arnold, Inc.
Glassware
Laboratory glassware is used to hold, pour, heat, and measure liquids. Most labs have many types of glassware. For example, flasks, beakers, petri dishes, test tubes, and specimen jars are used as containers. To measure the volume of a liquid, you use a graduated cylinder. The unit of measure for liquid volume is the liter (L) or milliliter (mL).
David Chasey/Getty Images
Compound Microscope
Microscopes enable you to observe small objects that you cannot observe with just your eyes. Usually, two types of microscopes are in science classrooms—dissecting microscopes and compound light microscopes, such as the one shown below. The girl is looking into two eyepieces to observe a magnified image of a small object or organism. However, some microscopes have only one eyepiece.
Microscopes can be damaged easily. It is important to follow your teacher’s instructions when carrying and using a microscope. For more information about how to use a microscope, see the Reference Handbook.
Lauren Burke/Getty Images
Computers—Hardware and Software
Computers process information. In science, you can use computers to compile, retrieve, and analyze data for reports. You also can use them to create reports and other documents, to send information to others, and to research information.
The physical components of computers, such as monitors and keyboards, are called hardware. The programs that you run on computers are called software. These programs include word processing, spreadsheets, and presentation programs. When scientists write reports, they use word processing programs. They use spreadsheet programs for organizing and analyzing data. Presentation programs can be used to explain information to others.
Richard T. Nowitz/CORBIS
Tools Used by Life Scientists
Magnifying Lens
A magnifying lens is a hand-held lens that magnifies, or enlarges, an image of an object. It is not as powerful as a microscope and is useful when great magnification is not needed. Magnifying lenses also can be used outside the lab where microscopes might not be available.
Stockbyte/Getty Images
Slide
To observe items using a compound light microscope, you must place it on a thin, rectangular piece of glass called a slide. You must handle slides gently to avoid breaking them.
Medicimage/Visulas Unlimited, Inc.
Dissecting Tools
Scientists use dissecting tools, such scalpels and scissors, to examine tissues, organs, or prepared organisms. Dissecting tools are sharp, so always use extreme caution when handling them.
Don Farrall/Getty Images
Pipette
A pipette is similar to an eyedropper. It is a small glass or plastic tube used to draw up and transfer liquids.
1. Key Concept Check What are some tools used by life scientists?
Hutchings Photography/Digital Light Source
Lesson AssessmentUse Vocabulary
1. Define description and explanation in your own words.
2. Use the term International System of Units (SI) in a sentence.
Understand Key Concepts
3. Which tool would a scientist use to view a tiny organism?
A. computer
B. compound microscope
C. test tube
D. triple-beam balance
4. Describe the difference between accuracy and precision.
5. Explain why scientists use significant digits.
6. Which is a quantitative observation?
A. 15 m long
B. red color
C. rough texture
D. strong odor
7. Which is one way scientists indicate how precise and accurate their experimental measurements
are?
are?
A. They keep accurate, honest records.
B. They make sure their experiments can be repeated.
C. They use significant figures in their measurements.
D. They record small samples of data.
Interpret Graphics
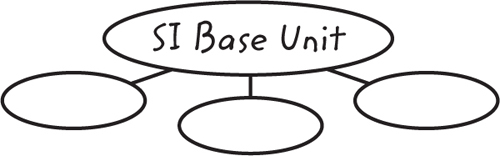
8. Draw a graphic organizer like the one below. Write the name of an SI base unit in each circle. Add additional circles to the graphic organizer as needed.
Critical Thinking
9. Recommend ways that computers can assist life scientists in their work.
Math Skills
10. Suppose you measure the mass of a book and it is 420.0890 g. How many significant digits are
in this measurement?
in this measurement?
11. How many significant figures are in 0.00840, 15.7, and 13.040?
